|
EN BREF
|
Le tableau des valeurs trigonométriques est un outil fondamental pour quiconque s’initie aux mathématiques, en particulier en trigonométrie. Comprendre comment utiliser ce tableau permet de restituer rapidement des valeurs clés telles que le sinus, le cosinus et la tangente pour les angles remarquables. À travers une analyse du cercle trigonométrique et des rapports trigonométriques, il devient possible d’appréhender les relations entre les différentes fonctions trigonométriques. Ce guide vous exposera des techniques pour mémoriser ces valeurs essentielles et vous donnera les clés pour naviguer aisément dans le monde de la trigonométrie.
Le tableau des valeurs trigonométriques est un outil fondamental en mathématiques, en particulier en trigonométrie. Il permet de déterminer rapidement les valeurs des fonctions trigonométriques telles que le sinus, le cosinus et la tangente pour des angles remarquables. Cet article vise à éclairer les notions essentielles relatives à l’utilisation de ce tableau et à en simplifier la compréhension pour une application pratique.
Les fonctions trigonométriques et leurs valeurs
Les fonctions trigonométriques principales sont le sinus (sin), le cosinus (cos) et la tangente (tan), mais on mentionne également des fonctions comme la cotangente, la sécante et la cosécante. Chacune de ces fonctions est liée à un angle dans un triangle rectangle. Par exemple, le sinus est défini comme le rapport entre le côté opposé à l’angle et l’hypoténuse, tandis que le cosinus est le rapport entre le côté adjacent à l’angle et l’hypoténuse. La tangente, quant à elle, est le rapport du sinus sur le cosinus.
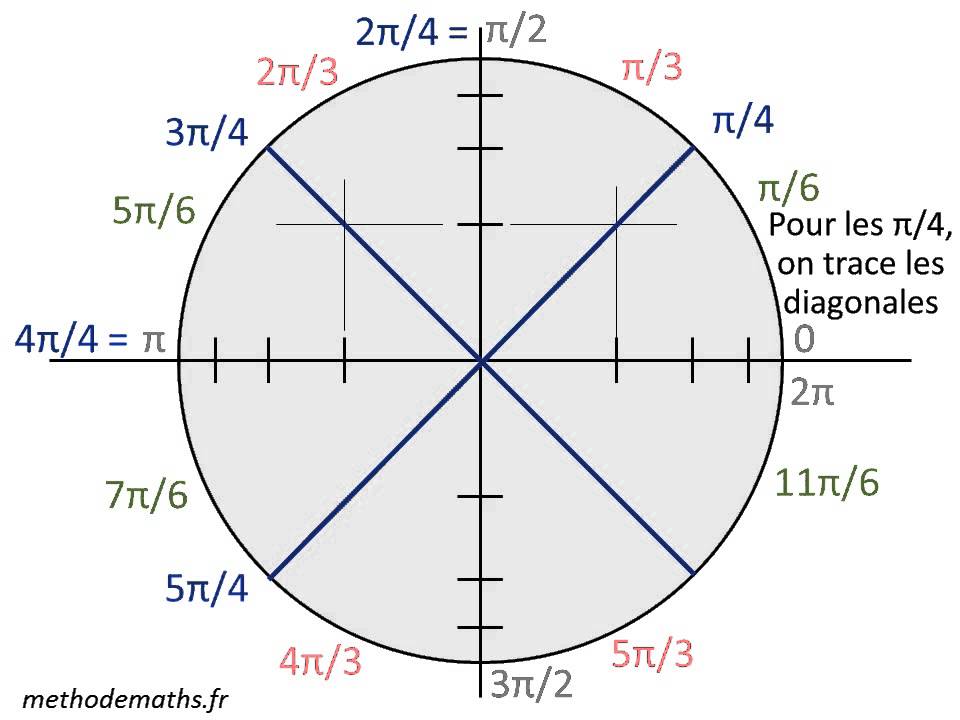
Le cercle trigonométrique
Pour mieux comprendre ces fonctions, il est essentiel d’introduire le concept du cercle trigonométrique. Le cercle trigonométrique permet de modéliser les angles et leurs corrélations avec les valeurs des fonctions trigonométriques. En traçant des rayons se déplaçant dans ce cercle, on peut facilement déterminer les coordonnées représentatives des angles. Cela facilite la restitution rapide des valeurs du sinus et du cosinus pour des angles précis.
Les angles remarquables
Les angles remarquables, tel que 0°, 30°, 45°, 60° et 90°, sont les plus souvent rencontrés. Chacun de ces angles a des valeurs spécifiques pour les fonctions trigonométriques. Par exemple, pour un angle de 30°, le sinus est égal à 1/2, alors que le cosinus est égal à √3/2. Le tableau des valeurs trigonométriques contient ces résultats, permettant ainsi de les retrouver facilement sans calcul.
Méthodes pour mémoriser le tableau des valeurs trigonométriques
Il existe plusieurs techniques pour faciliter la mémorisation des valeurs présentes dans le tableau des valeurs trigonométriques. Une méthode efficace consiste à utiliser un tableau organisé, généralement de 6 lignes et 6 colonnes, qui classe les fonctions trigonométriques en fonction des degrés. Tracer ce tableau aide à visualiser les relations entre les différentes valeurs et à mémoriser plus aisément l’ensemble des résultats.
Utilisation pratique du tableau des valeurs trigonométriques
Le tableau des valeurs trigonométriques est vital dans de nombreux domaines des mathématiques. Que ce soit en géométrie, en physique, ou encore en ingénierie, connaître les valeurs des fonctions trigonométriques permet d’effectuer des calculs rapides et précis. Il sert également d’outil d’aide lors de la résolution de problèmes complexes nécessitant des estimations d’angles ou de distances.
Démonstrations essentielles
Pour toute personne intéressée par la trigonométrie, il est également utile de connaître les démonstrations des formules trigonométriques fondamentales. Cela va au-delà de la simple mémorisation et permet une compréhension approfondie des propriétés de ces fonctions. Les démonstrations aident à établir des connexions entre les différentes valeurs du tableau et à en saisir pleinement l’utilité.
Les applications numériques et graphiques
Aujourd’hui, les outils numériques facilitent grandement l’accès aux tableaux trigonométriques ainsi qu’à des outils graphiques. En utilisant des applications ou des logiciels, il est possible de tracer des graphes de fonctions trigonométriques, et d’évaluer facilement les valeurs pour n’importe quel angle, rendant ainsi l’apprentissage plus efficace et interactif.
| Fonction | Valeurs aux angles remarquables |
| Sinus | 0, 1/2, √2/2, √3/2, 1 |
| Cosinus | 1, √3/2, √2/2, 1/2, 0 |
| Tangente | 0, √3/3, 1, √3, indéfini |
| Cosécante | indéfini, 2, √2,√3/3, 1 |
| Sécante | 1, 2/√3, √2, 2, indéfini |
| Cotangente | indéfini, √3, 1, √3/3, 0 |
Le tableau des valeurs trigonométriques est un outil essentiel en mathématiques qui permet de restituer rapidement les valeurs du sinus, du cosinus et de la tangente pour les angles remarquables. Cet article vous guide à travers les notions fondamentales de la trigonométrie et vous montre comment utiliser efficacement ce tableau.
Introduction à la trigonométrie
La trigonométrie est une branche des mathématiques qui traite des relations entre les côtés et les angles des triangles. Le cercle trigonométrique joue un rôle fondamental en permettant de modéliser ces relations. En étudiant ce cercle, on peut déterminer les coordonnées des points situés sur sa périphérie, se traduisant ainsi en valeurs précises pour les différentes fonctions trigonométriques.
Les fonctions trigonométriques principales
Les fonctions trigonométriques les plus courantes sont le sinus (sin), le cosinus (cos) et la tangente (tan). Chacune de ces fonctions a ses propres caractéristiques et applications. Par exemple, le sinus représente le rapport entre le côté opposé à un angle et l’hypoténuse, tandis que le cosinus est le rapport entre le côté adjacent et l’hypoténuse. La tangente, quant à elle, est le rapport entre le sinus et le cosinus.
Utilisation du tableau des valeurs trigonométriques
Le tableau des valeurs trigonométriques vous permet de retrouver rapidement des valeurs importantes sans avoir à faire des calculs complexes. En vous familiarisant avec ce tableau, vous pouvez facilement déterminer les valeurs du sinus, du cosinus et de la tangente pour des angles comme 0°, 30°, 45°, 60° et 90°. Il existe également des versions du tableau en degrés et en radians, s’adaptant ainsi à divers contextes mathématiques.
Techniques de mémorisation
Pour faciliter l’apprentissage du tableau des valeurs trigonométriques, certaines techniques peuvent être mises en place. Par exemple, tracer un tableau avec 6 lignes et 6 colonnes peut aider à visualiser les différentes fonctions. Vous pouvez également utiliser des moyens mnémotechniques pour retenir les valeurs des angles remarquables et leurs rapports trigonométriques.
Importance des rapports trigonométriques
Les rapports trigonométriques, à savoir le sinus, le cosinus et la tangente, sont cruciaux dans de nombreuses applications mathématiques et scientifiques. Ils sont fréquemment utilisés pour résoudre des problèmes géométriques, physiques et d’ingénierie. Une bonne maîtrise de ces concepts vous permettra d’aborder des sujets plus avancés avec confiance.
- Signification : Représentation des valeurs de sinus, cosinus, et tangente pour des angles spécifiques.
- Angles remarquables : Les valeurs pour 0°, 30°, 45°, 60°, et 90° sont essentielles.
- Cercle trigonométrique : Modélise les fonctions trigonométriques sur la périphérie d’un cercle.
- Mémoire : Techniques pour retenir les valeurs sans effort.
- Applications : Utilisées en physique, ingénierie et architecture.
- Fonctions principales : Incluent sinus, cosinus, tangente et leurs réciproques.
- Démonstrations : Essentielles pour prouver les relations entre des triangles.
- Utilisation pratique : Outils pour résoudre des problèmes géométriques complexes.
- Tableau PDF : Disponibilité de tableaux complets en formats PDF pour une consultation facile.
- Radian vs Degré : Comprendre la relation entre ces deux unités pour une utilisation correcte.
Introduction au tableau des valeurs trigonométriques
Le tableau des valeurs trigonométriques est un outil essentiel en mathématiques pour ceux qui cherchent à naviguer dans le monde de la trigonométrie. Comprendre et utiliser ce tableau permet d’obtenir rapidement les valeurs exactes des fonctions trigonométriques pour divers angles, facilitant ainsi la résolution de problèmes complexes. Cet article vous guidera à travers les concepts fondamentaux de la trigonométrie, les rapports trigonométriques, et des techniques pratiques pour optimiser la mémorisation de ces valeurs importantes.
Les fonctions trigonométriques fondamentales
Les fonctions trigonométriques les plus courantes sont le sinus, le cosinus, et la tangente. Chacune de ces fonctions est définie à partir d’un triangle rectangle, où le sinus est le rapport entre le côté opposé et l’hypoténuse, le cosinus le rapport entre le côté adjacent et l’hypoténuse, et la tangente le rapport entre le côté opposé et le côté adjacent. Une compréhension claire de ces rapports est essentielle pour utiliser efficacement le tableau trigonométrique.
Le rôle du cercle trigonométrique
Le cercle trigonométrique facilite la compréhension des valeurs des fonctions trigonométriques. En modélisant les points sur la périphérie du cercle, il devient plus simple de déterminer les coordonnées qui correspondent à différents angles. En utilisant le cercle, vous pouvez visualiser comment le sinus et le cosinus des angles se rapportent entre eux, ce qui enrichit votre compréhension des transformations et des comportements de ces fonctions.
Comment mémoriser le tableau des valeurs
Mémoriser les valeurs trigonométriques peut s’avérer compliqué. Pour y parvenir, une méthode efficace consiste à tracer un tableau comportant six lignes et six colonnes. Dans ce tableau, placez les fonctions trigonométriques dans la première colonne à partir de la deuxième ligne. En structurant les valeurs de manière claire, vous pourrez mieux visualiser et retenir les relations entre les différentes fonctions pour des angles particuliers.
Les angles remarquables
Les angles remarquables, tels que 0°, 30°, 45°, 60° et 90°, sont essentiels dans le cadre des valeurs trigonométriques. Ces angles ont des valeurs spécifiques et bien connues pour le sinus, le cosinus et la tangente. Par exemple, on sait que le sinus de 30° est 1/2, le cosinus de 60° est aussi 1/2 et la tangente de 45° est 1. Connaître ces valeurs vous permettra d’effectuer des calculs trigonométriques plus facilement.
Utilisation pratique du tableau
Utiliser le tableau des valeurs trigonométriques dans des exercices mathématiques et des problèmes réalistes peut sembler intimidant, mais cela devient simple avec un peu de pratique. Lors de la résolution de problèmes, commencez par identifier l’angle dont vous avez besoin et ensuite, consultez le tableau pour obtenir directement la valeur du sinus, du cosinus ou de la tangente associée. Ce processus vous aide non seulement à gagner du temps, mais aussi à éviter d’éventuelles erreurs dans les calculs.
L’importance des formules trigonométriques
En complément du tableau, il est crucial de maîtriser les formules trigonométriques pour les concours et examens. La compréhension des relations entre les différentes fonctions trigonométriques, telles que les identités et les formules de transformations, enrichit votre capacité à résoudre des équations et à analyser différents types de problèmes. Les démonstrations de ces formules vous fourniront une connaissance en profondeur qui vous servira tout au long de votre parcours en mathématiques.